[LeetCode From Day One] - Floyd Cycle Detection

发表于 · 归类于 Algorithm  · 阅读量 加载中...

Floyd环路检测算法，又称龟兔赛跑算法（Tortoise and Hare Algorithm），是Robert W. Floyd在上世纪60年代发明的在线性时间内检测单链表，有限状态机（FSM）或者迭代函数中是否存在环路的算法。最简单的一个检测环路的方法就是遍历链表，记录已被访问的节点，如果某个节点的访问次数超过1，则表明存在环路，时间复杂度为$O(n^2)$。而Floyd算法可以在线性时间内检测环路。其算法基本思想是如果链表存在环路，那么在环上以一快一慢不同速度前进的两个指针一定会相遇，并且算法可以求出相遇处所在环的起点与长度。下图是一个简单的算法示意图。

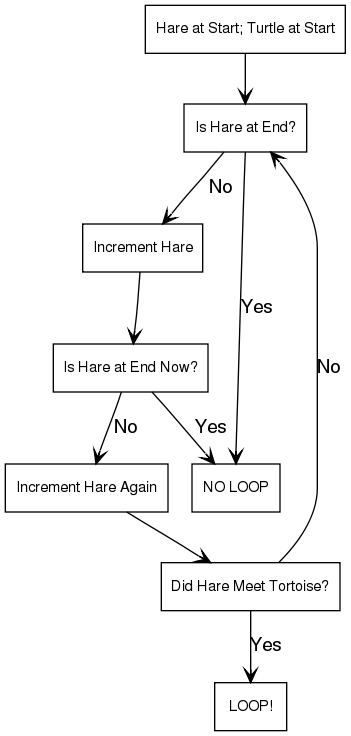floyd （图片Credit：Floyd’s Cycle Detection Algorithm (The Tortoise and the Hare)）龟兔赛跑可能是最著名的环路检测算法，同时也是一个非常直观的例子。Tortoise和Hare是两个指针，同时从链表的头部出发。每次迭代，Tortoise爬得比较慢，只能往前走一步，Hare则能前进两步。如果链表存在环，Hare最终会绕圈跑，可能不止一圈，但是在Tortoise进入这个loop之后，Hare最终都会与Tortoise相遇。如果单链表中无环，显然Hare会率先达到链表末尾，算法退出。算法时间复杂度为$O(n)$，空间复杂度为常数，$O(1)$。

对FSM与链表应用Floyd Cycle Detection算法，可以判断从某个初态/起点开始是否会返回到一个已访问过的状态/节点。而对于迭代函数来说，则可以判断其是否存在周期，以及求出最小正周期。下面以几个LeetCode题目为例，用代码解释Floyd环路算法。

Linked List Cycle

本题在之前的双指针II其实已经介绍过，是对Floyd Cycle Detection算法最直观的解释，对题目解法不再详述，这里仅结合本例解释算法如何求得环长度以及相遇点。

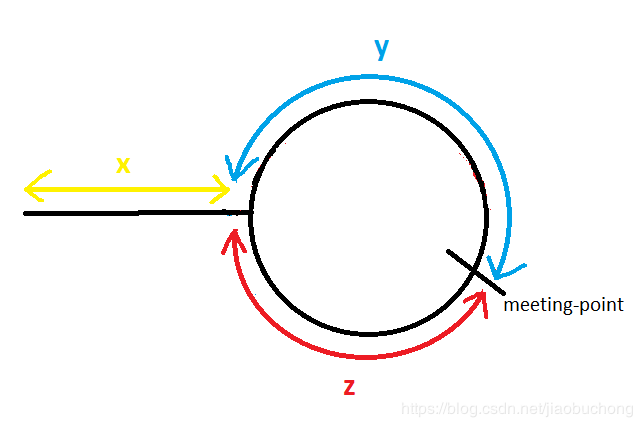
linkedlist

上图中黑色线条表示包含环路的单链表，左端为链表头部。到meeting-point位置，慢指针走过的距离为x+y，而快指针走过的距离为x+y+z+y，即x+2y+z。由于快指针的速度是慢指针的两倍，所以2(x+y)=x+2y+z，即x=z，x代表的就是非环的长度。在相遇点固定快指针，接着移动慢指针，直至慢指针再次到达meeting-point，走过的距离就是环的长度。

Happy Number

本题是LeetCode简单难度202题Happy Number，是Floyd Cycle Detection算法对迭代函数的一个应用。

实现一个算法判断给定的正整数是否是Happy Number。Happy Number指的是不断计算各位数字的平方和，直到平方和等于1，或者一直循环（即计算得到某个已经计算过平方和的数）。 Example：
    Input: 19
    Output: true
    Explanation:
        $1^2+9^2=82$
        $8^2+2^2=68$
        $6^2+8^2=100$
        $1^2+0^2+0^2=1$

根据题意，直接可以想到用HashSet解决，每次迭代计算产生的数加到HashSet中，如果遇到相同的数，跳出循环，判断该数是否为1。

class Solution {
    public int sumOfSquares(int n) {
        int sum = 0;
        while(n != 0) {
            sum += (n%10)*(n%10);
            n /= 10;
        }
        return sum;
    }

    public boolean isHappy(int n) {
        Set<Integer> set = new HashSet<Integer>();
        int squareSum,remain;
        while (set.add(n)) {
            squareSum = sumOfSquares(n);
            if (squareSum == 1)
                return true;
            else
                n = squareSum;
    
        }
        return false;
    }
}

本题同样可以对函数sumOfSquares应用Floyd算法，慢指针一次迭代调用一次sumOfSquares，快指针计算两次。

class Solution {
    public int sumOfSquares(int n) {
        int sum = 0;
        while(n != 0) {
            sum += (n%10)*(n%10);
            n /= 10;
        }
        return sum;
    }
    public boolean isHappy(int n) {
        int slow=n, fast = n;
        do {
            slow = sumOfSquares(slow);
            fast = sumOfSquares(fast);
            fast = sumOfSquares(fast);
        } while(slow != fast);
        if(slow == 1) return true;
        return false;
    }
}

算法的改进

Brent在1980年提出的环路检测算法同样有着线性的时间复杂度，但是步数比Floyd的要少24%~36%左右。有兴趣的可以参考Brent’s Cycle Detection Algorithm (The Teleporting Turtle)。

  #LeetCode 
« Bit Manipulation in Java [LeetCode From Day One] - Prime Number »
☰