Bit Manipulation in Java
处理byte,int,float,double,string或者其他复杂类型的数据结构对于程序员来说应该是比较熟悉的。在计算机中,不管什么类型的数据都是以二进制的形式存储的。位运算就是对内存中的二进制数进行操作,是一组很基础的操作,并且有着很快的速度(代码可读性稍微差点。本文对一些基本的位运算做一个总结,并且讨论几个LeetCode上关于Bit Manipulation的算法题。最后参考了一些博文,记录了一些位运算的技巧,正确应用这些技巧有时能达到四两拨千斤的效果。
原码、反码、补码
在第一篇LeetCode From Day One系列的文章中,博主总结过32位机器上C++各数据类型的表示范围。对于C++来说,不同的操作系统平台给基本数据分配的字节是不一样的。而对于Java这种跨平台语言来说,JVM给基础数据分配的字节数是一致的。
| 类型 | 字节 | 类型 | 字节 |
|---|---|---|---|
| int | 4字节 | float | 4字节 |
| short | 2字节 | double | 8字节 |
| long | 8字节 | char | 1字节 |
| byte | 1字节 | boolean | 1位 |
可以看到一个int类型占4字节,也就是32位。需要注意的是整数类型的最高位是符号位,0表示正数,1表示负数。为了方便计算(做减法运算),在计算机中用补码表示整数。原码、反码、补码这几个概念在计算机原理这门课学过,这里简单做个回顾,以下均以int类型为例。
原码 一个数字的二进制表示即是它的原码。
7 = 00000000 00000000 00000000 00000111(原)
反码
- 正数的反码是其本身
- 负数的反码是在原码的基础上,符号位不变,其余位取反
7 = 00000000 00000000 00000000 00000111(反)
-7 = 11111111 11111111 11111111 11111000(反)
反码直接将符号位存储在整个结构中,计算机在计算过程中不必去判断符号选择加减法,只需要对两个数做加法即可。
7 = 00000000 00000000 00000000 00000111(反)
+
-7 = 11111111 11111111 11111111 11111000(反)
=
11111111 11111111 11111111 11111111(反)
=
10000000 00000000 00000000 00000000(原)
=
-0
用反码进行加法运算可能会出现-0和+0的情况,所以又引入了补码。
补码
- 正数的补码是其本身
- 负数的补码是其反码值保持符号位不变,末位加1
7 = 00000000 00000000 00000000 00000111(补)
-7 = 11111111 11111111 11111111 11111001(补)
再用补码计算7+(-7)。
7 = 00000000 00000000 00000000 00000111(补)
+
-7 = 11111111 11111111 11111111 11111001(补)
=
100000000 00000000 00000000 00000000(补)
=
00000000 00000000 00000000 00000000(原)
=
0
计算结果最左端产生的进位由于超出了int类型的表示范围,故直接舍弃。注意补码计算的结果仍旧位补码,要得到原码,对计算结果再求一次补码即可。(补码的补码是原码
Java中的位操作
Java位运算包括与、或、非、异或、左移、右移、逻辑右移(无符号),需要注意的是Java的原始类型不包含无符号类型,所以需特地指明无符号右移运算。C/C++统一使用右移操作,编译器针对数据类型(unsigned or signed)决定使用有符号还是无符号的右移操作。下表简单总结C与Java中的位运算。
| 运算 | C | Java | 规则 |
|---|---|---|---|
| 按位与 | & | & | 两位都为1,结果为1;否则为0 |
| 按位或 | | | | | 至少一位为1,结果为1;否则为0 |
| 按位取反 | ~ | ~ | 0变1;1变0 |
| 按位异或XOR | ^ | ^ | 相同为0;不同为1 |
| 左移 | « | « | 向左移动固定位,末尾添0 |
| 右移(有符号) | >> | >> | 向右移动固定位,高位补符号位 |
| 逻辑右移(无符号) | >>> | 向右移动固定位,高位永远补0 |
注意,位操作符只能应用于整型数据,对于浮点型进行位操作会报错。方便起见,以下将整型简化位1字节也就是8位。
位运算符 &、|、~、^、<<、>>、>>>
按位与 &
对应位都为1,则输出结果也为1;否则为0。
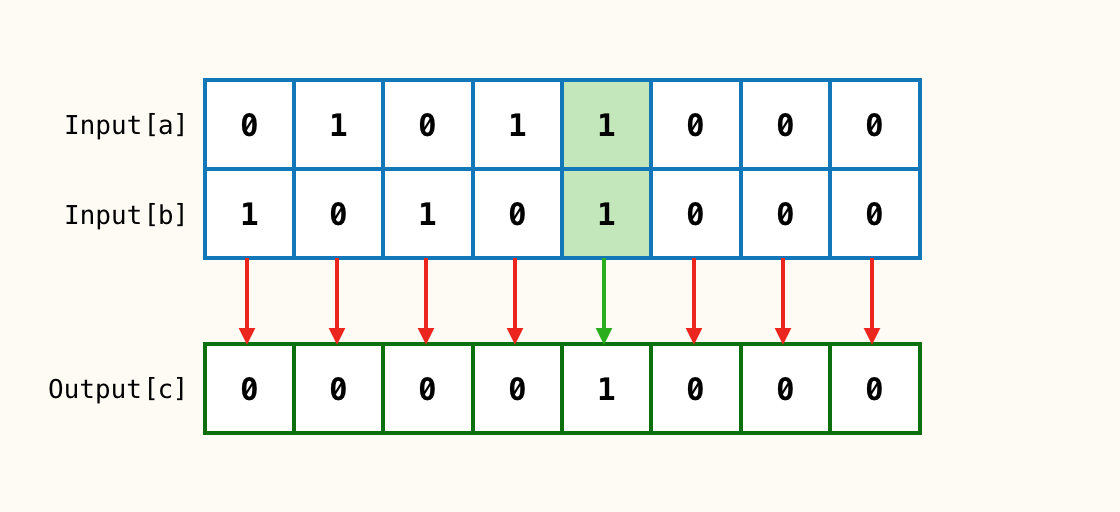
按位或 |
对应位只要有一个为1,则结果为1;若两位都为0,则结果为0。
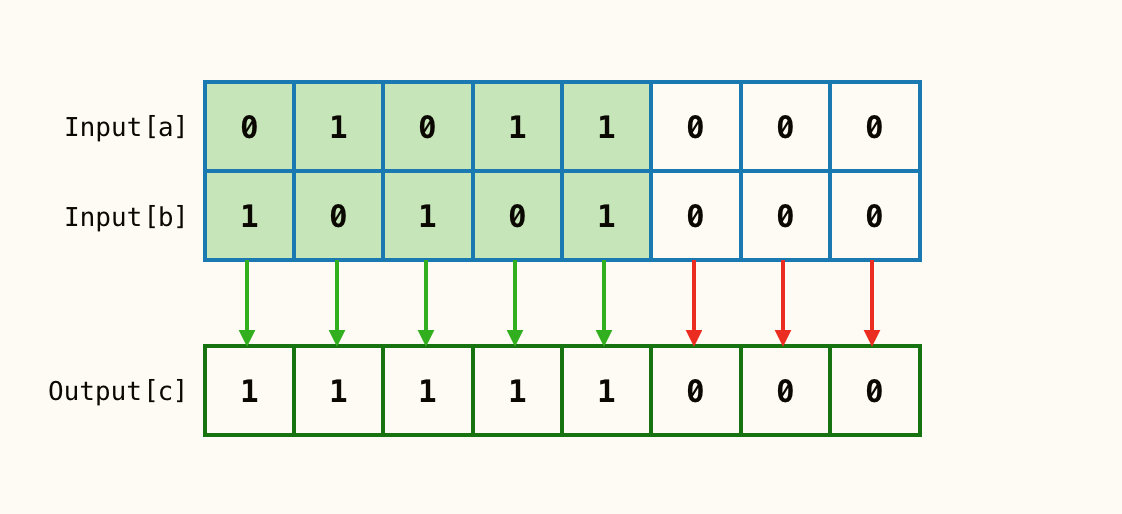
按位取反 ~
按位取反或者叫非,属于一元操作符,也是位操作里面唯一一个一元操作符,只有一个参数。将对应位的0变成1,1变成0。
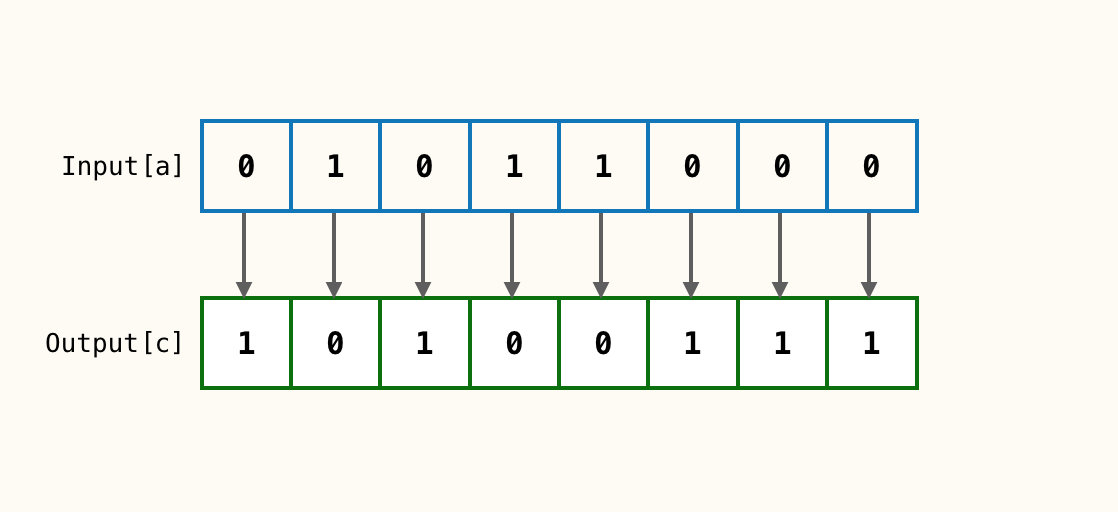
按位异或^
两个整数进行异或时,对应位的值不同,则结果为1,否则为0。
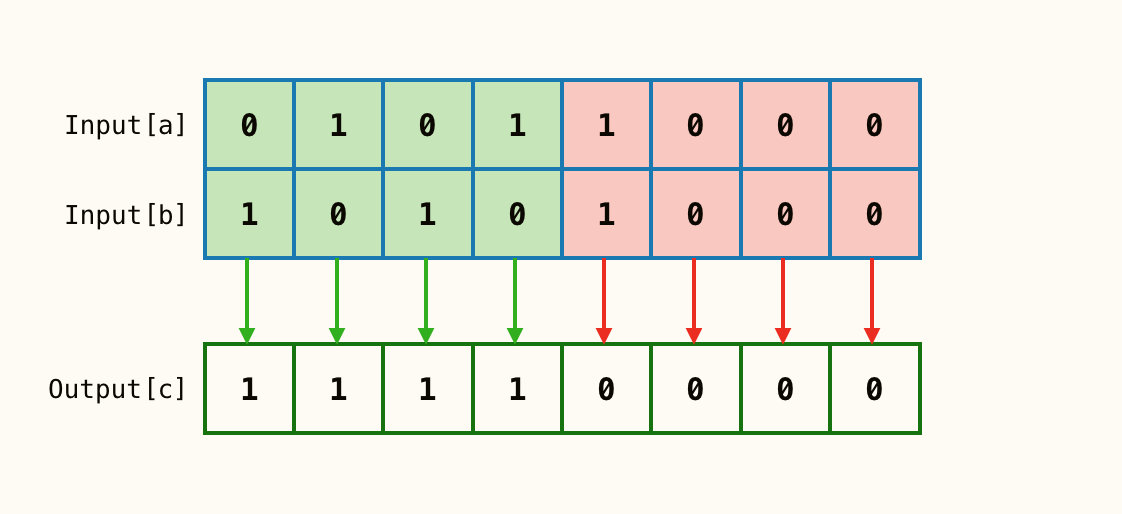
例如a^a=0,a^0=a。
左移 <<
左移是一个二元操作符,它将给定的二进制数整体向左移动固定位,舍弃高位超出限制的位,并在末尾补0。左移k位相当于数乘以$2^k$。
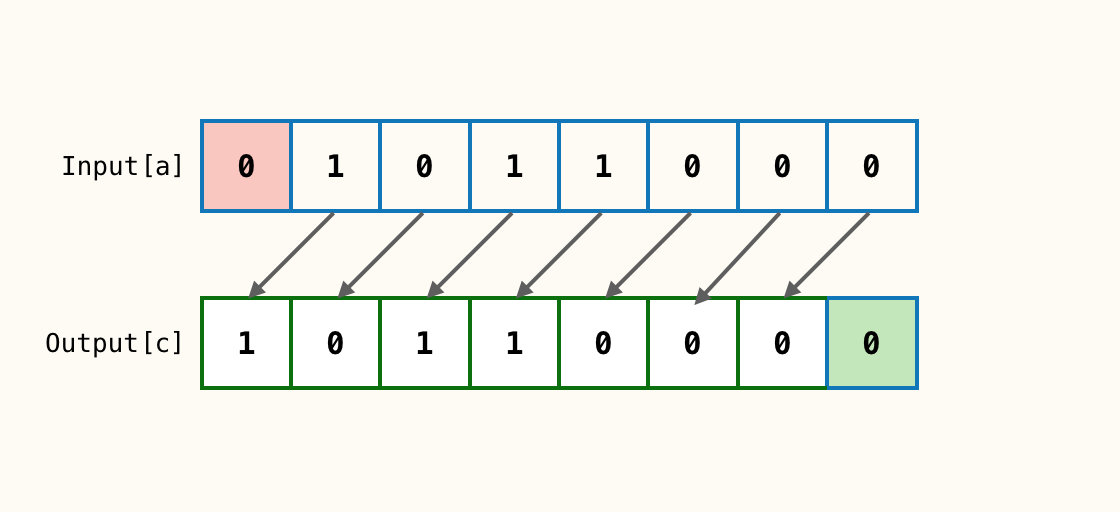
带符号右移 >>
右移同样是一个二元操作符,它将给定的二进制数整体向右移动固定位,舍弃低位,并在高位补符号位。右移k位相当于数除以$2^k$。
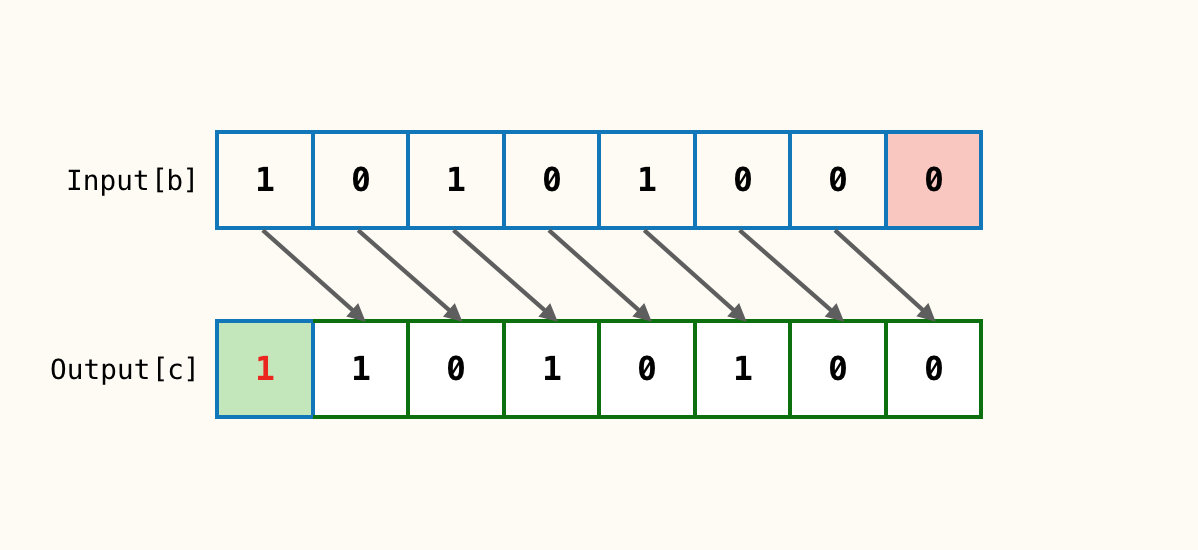
逻辑右移(无符号)>>>
逻辑右移是Java中新增的一种无符号的右移操作符。做法是将数的全部位包括符号位右移固定位,舍弃地位,并且不管符号位如何,永远在高位补0。
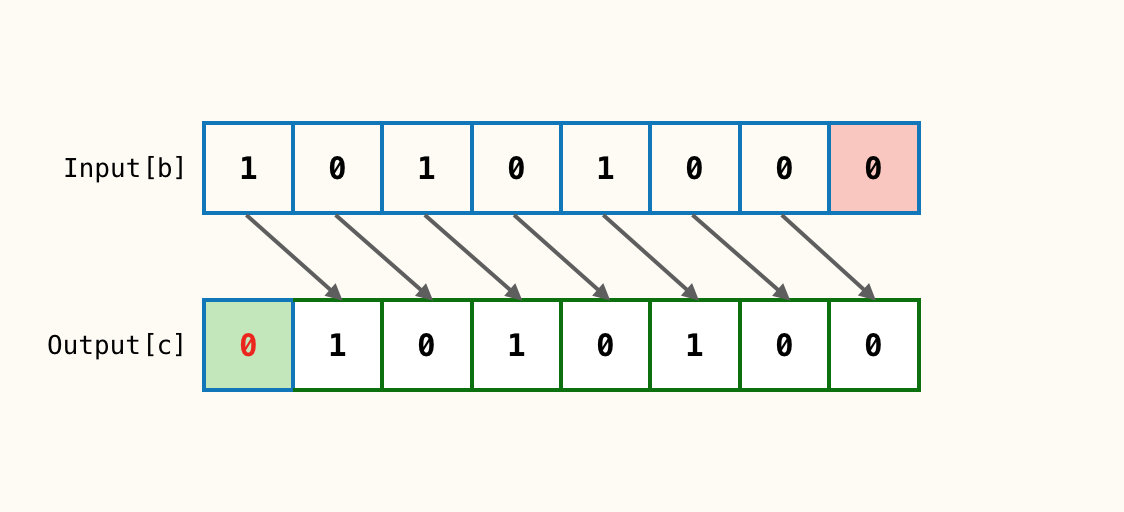
以上例子的图片均来源于大天狗子的博客,感谢提供如此简单明了的例子。
基于位运算的算法
位运算的应用有很多,包括但不限于空间压缩,交换两数,power set(所有子集)等。这里介绍几个常用的以及LeetCode上遇到的题。
Single Number
LeetCode简单难度的136题出现一次的数。
给定一个非空的整数数组, 除一个数以外的所有数都出现两次,找到并返回出现一次的那个数。 Example:
Input: [2,2,1] Output: 1
看似很简单的一道题,用个hashmap就解决了,时间复杂度$O(n)$,空间复杂度$O(n)$。
class Solution {
public int singleNumber(int[] nums) {
Map<Integer, Integer> map = new HashMap<>();
for(int i = 0; i < nums.length; ++i) {
if(map.containsKey(nums[i])) map.remove(nums[i]);
else map.put(nums[i], 1);
}
return Integer.parseInt(map.keySet().toArray()[0].toString());
}
}
但是注意,题目进一步要求能否在不开辟额外存储空间的前提下实现。这就要用到一点位操作的知识了。异或XOR操作有这样几个特性,两个相同的数的异或结果是0,即x^x=0;一个数与0的异或结果还是这个数本身,即x^0=x。基于这两个性质,我们可以对数组的所有元素求异或,由于出现两次的数异或后都等于0,所以最后的结果必定是出现一次的数与0异或的结果,即它本身。
class Solution {
public int singleNumber(int[] nums) {
for(int i = 1; i < nums.length; ++i) {
nums[0] = nums[0] ^ nums[i];
}
return nums[0];
}
}
Subsets
LeetCode中等难度78题求幂集。
给定一个包含不同元素的整数集合,返回其所有子集(幂集)。 Example:
Input: [1,2,3]
Output: [[], [1], [1,2], [1,3], [2], [2,3], [3], [1,2,3]]
一般来说,一开始不太容易想到用位操作来解这题。一个比较容易想到的办法就是每遍历一个数,就把该数与现有的每个子集合并,形成几个新的子集,添加到最后的结果当中去。还是以题目中的输入为例:
- 首先初始化一个空集
[]; - 读取
1,与空集合并成[1]形成一个新的子集,最终结果变为[[], [1]]; - 读取
2,与现有子集逐一合并,得到[[2], [1,2]],返回结果变为[[], [1], [2], [1,2]]; - 读取
3,同理得到最后的结果,[[], [1], [1,2], [1,3], [2], [2,3], [3], [1,2,3]];
给出Java实现代码。
class Solution {
public List<List<Integer>> subsets(int[] nums) {
List<List<Integer>> result = new ArrayList<>();
List<Integer> empty_set = new ArrayList<>();
result.add(empty_set);
for(int i = 0; i < nums.length; ++i) {
int prev_size = result.size();
for(int j = 0; j < prev_size; ++j) {
List<Integer> subset = new ArrayList<>(result.get(j));
subset.add(nums[i]);
result.add(subset);
}
}
return result;
}
}
我们知道,任意给定包含n个元素的集合共有$2^n$个子集。我们可以用一个二进制位表示集合中的元素属于给定的子集,1表示在子集中,0表示不在。仍然以[1,2,3]为例,二进制码从低位到高位分别表示1,2,3:
- $0=(000)_2={}$
- $1=(001)_2={1}$
- $2=(010)_2={2}$
- $3=(011)_2={1,2}$
- $4=(100)_2={3}$
- $5=(101)_2={1,3}$
- $6=(110)_2={2,3}$
- $7=(111)_2={1,2,3}$
为了判断某个数是否在当前子集中,即该位的值是否位1,可以采用右移操作,在与上1得到某一位的值。代码如下:
class Solution {
public List<List<Integer>> subsets(int[] nums) {
List<List<Integer>> result = new ArrayList<>();
for(int i = 0; i < (1 << nums.length); ++i) {
List<Integer> subset = new ArrayList<>();
for(int j = 0; j < nums.length; ++j) {
if(((i >> j) & 1) > 0) subset.add(nums[j]);
}
result.add(subset);
}
return result;
}
}
Number of 1 Bits
LeetCode简单难度191题求一个无符号整数中1的个数。
给定一个无符号整数,返回其二进制表示中1的个数。 Example:
Input: 00000000000000000000000000001011
Output: 3
利用n & (n-1)不断消去最右边的1,直到n变为0,记录消去1的次数就是题解。
public class Solution {
// you need to treat n as an unsigned value
public int hammingWeight(int n) {
int weight = 0;
while(n != 0) {
n = (n & (n-1));
++weight;
}
return weight;
}
}
Sum of Two Integers
LeetCode简单难度371题计算两个整数的和要求不使用四则运算计算两个整数的和,自然想到使用位运算完成加法运算。二进制的运算其实与整数的运算很相似,每一位的和加上进位即是最终的答案。对二进制数来说,只有1和1的和会产生进位10。其余情况都可以看作是异或操作的结果。对于进位的结果,可以看作是两数相与之后左移一位的结果。所以我们不断计算异或操作与进位操作的和,直到进位的结果为0。
class Solution {
public int getSum(int a, int b) {
int sum;
int carry;
while(b != 0) {
sum = a ^ b;
carry = (a & b) << 1;
a = sum;
b = carry;
}
return a;
}
}
举个简单的例子来说,假设要计算6+7的和,即00000110+00000111:
- 第一步计算
00000110 ^ 00000111 = 00000001; - 第二步计算进位
(00000110 & 00000111) << 1 = 00000110 << 1 = 00001100; - 计算异或结果与进位结果的和
000000001 ^ 00001100 = 00001101; - 再次计算进位
(00000001 & 00001100) << 1 = 00000000; - 最终结果为
00001101,即13;
Tricks
判断奇偶 一个整数的奇偶性由其二进制表示的最后一位决定,0表示偶数,1表示奇数。x&1 == 0即可判断。
交换两数
a ^= b;
b ^= a;
a ^= b;
相反数 利用位操作可变换整数的符号,只需对数取反再加1,~x+1。
最右边的1 x&(x-1)可以消去最右边的1。利用这个技巧可以判断一个数是否为2的幂(LeetCode简单难度231题Power of Two)。思路是一个数如果是2的幂次,一定大于0并且二进制表示只包含一个1。利用x&(x-1)消去最右边的1之后应该返回0。
class Solution {
/**
* Iterative
*/
// public boolean isPowerOfTwo(int n) {
// if(n == 1) return true;
// long power = 1;
// while(power < n) {
// power *= 2;
// if(power == n) return true;
// }
// return false;
// }
/**
* Bit manipulation
*/
public boolean isPowerOfTwo(int n) {
if(n <= 0) return false;
return (n&(n-1)) == 0;
}
}
低位到高位取第k位 使用右移操作,(x>>(k-1))&1。
设置第k位为1 x|(x<<(k-1))
还有些技巧在上一小节的算法中都已经包含了。