[LeetCode From Day One] - Prime Number
素数是大于1并且不再有除1和它本身外的因数的数,否则为合数。围绕素数主要有两个基本问题,i) 求小于n的所有素数;ii) 判断一个数n是否为素数。本为结合LeetCode简单难度204题素数的个数介绍几种解决问题i)的算法。
首先给出素数的几个基本性质:
- 算术基本定理,任何一个大于1的自然数n都可以分解为有限个质数的乘积;
- 若一个数n可以进行因数分解,则得到的两个数必定一个大于等于$\sqrt{n}$,一个小于等于$\sqrt{n}$;
- 素数定理,小于n的素数个数为$\frac{n}{\ln{n}}$;
Brute-force solution
根据素数的定义我们可以给出一种暴力解法给出所有小于n的素数,其基本想法就是素数判定plus数组遍历。下面给出的是优化了判定范围与步长的代码。根据第二个性质,判断一个素数是否为素数,只需判断n能否被$[2,\sqrt{n}]$范围内的数整除。又除2以外的偶数一定不是素数,故步长设定为2,判断所有的奇数。
class Solution {
/**
* 暴力解法 O(n*sqrt(n))
*/
public int countPrimes(int n) {
int cnt = 0;
for(int i = 2; i < n; ++i) {
if(isPrime(i)) ++cnt;
}
return cnt;
}
public boolean isPrime(int n) {
if(n == 2) return true;
if(n < 2 || x % 2 == 0) return false;
for(int i = 3; i <= Math.sqrt(n); i+=2) {
if(n % i == 0) return false;
}
return true;
}
}
该算法时间复杂度为$O(n\sqrt{n})$,空间复杂度$O(1)$,耗时长。
Sieve of Eratosthenes
埃拉托斯特尼筛数法是一种古老却简单的找到小于n的所有素数的算法。该算法利用已找到的素数,筛去所有该素数的倍数。下面的动图(Credit:Wikipedia)很好地解释了该算法的原理。
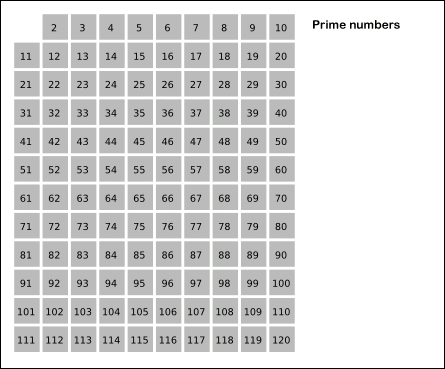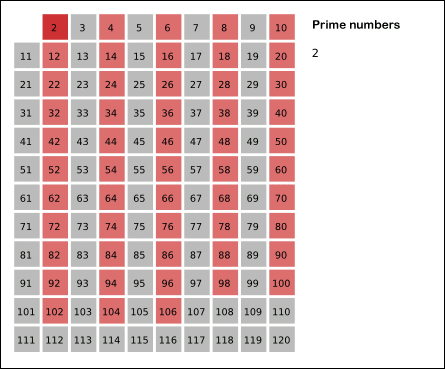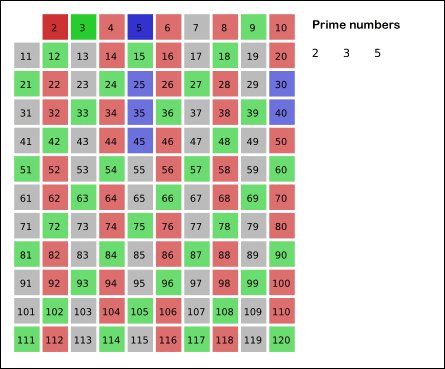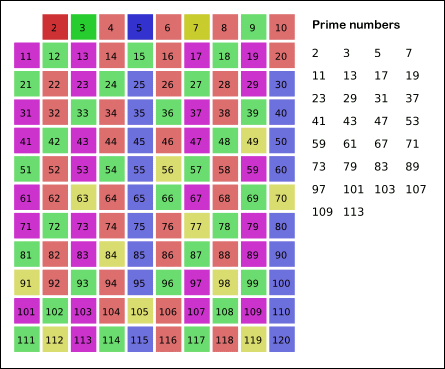
埃式筛数法有以下几个步骤:
- 初始化一张素数表,例如一个boolean数组,
true/false值表示该数是否为素数; - 从最小的素数2开始,把下标为2,4,6,…的值置为
false; - 找到大于2的最小素数,即下标对应的值为
true,重复2步骤; - 算法退出后,素数表中值为
true的即为所有小于n的素数;
为了少一个for循环把boolean数组所有值设置为true,我们使用notPrime数组,false为默认值,表示是素数,true则表示非素数,代码如下。嵌套的for循环条件要注意整型溢出(i*i可能超过int的表示范围),采用long。
class Solution {
/**
* 埃拉托斯特尼筛法 O(n*ln(lnn))
*/
public int countPrimes(int n) {
boolean[] notPrime = new boolean[n+1];
int cnt = 0;
for(int i = 2; i < n; ++i) {
if(!notPrime[i]) {
++cnt;
for(long j = (long)i*i; j < n; j+=i) {
notPrime[(int)j] = true;
}
}
}
return cnt;
}
埃式筛数法的时间复杂度为$O(n\ln{\ln{n}})$,已经近似$O(n)$,空间复杂度由于开辟了一个布尔数组,故为$O(n)$,具体的证明有兴趣的可以戳普通筛法时间界的证明。
Euler’s Sieve
我们进一步可以观察到,有些合数被其每个质因子重复筛选了好几次,比如6,被质因子2与质因子3分别筛选了一次。欧拉筛数法改进了这一点,考虑是否筛出一个数时,只由它的最小质因子来判断,使得每个合数只被筛选一次。欧拉筛数的时间复杂度是线性的$O(n)$。
class Solution {
/**
* 欧拉筛法 O(n)
*/
public int countPrimes(int n) {
boolean[] notPrime = new boolean[n+1];
int[] primes = new int[n+1];
int cnt = 0;
for(int i = 2; i < n; ++i) {
if(!notPrime[i]) {
primes[cnt++] = i;
}
for(int j = 0; j < cnt && primes[j]*i < n; ++j) {
notPrime[primes[j]*i] = true;
if(i % primes[j] == 0) break; //再往后就不是最小质因子了
}
}
return cnt;
}
}