[LeetCode From Day One] - 572. Subtree of Another tree
本篇文章分析LeetCode简单难度572题,判断一棵树是否为另一棵树的子树。这题也是包括facebook,google在内的大公司考察的关于树的经典题目。
给定两颗非空的二叉树
s与t,写一个函数判断t是否与s的某颗子树有着相同的结构。 Example: given tree s and t:
3 4
/ \ / \
4 5 1 2
/ \
1 2
Output: true
s的子树由s中的任意一个节点以及该节点的所有子孙节点组成。s本身也是s的子树。
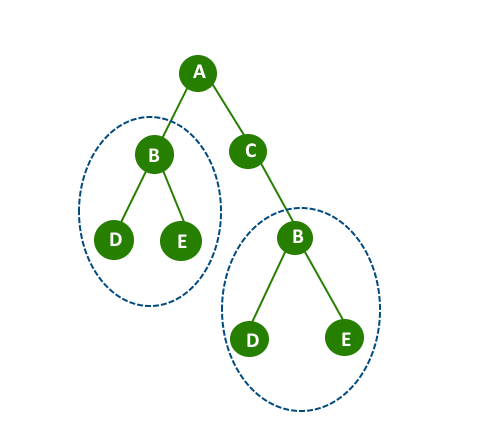
本文提供两种思路,分别是遍历s,判断以遍历节点为根节点的子树与t是否相同和前序遍历s与t,判断t的遍历结果是否为s的字串。
遍历s
先看第一种方式,比较直观。首先我们递归地在s中找到与t根节点值相同的节点(if(s.val == t.val)。之后再递归地(isEqual)判断以该节点为根节点构成的子树与t是否相同。递归函数isEqual中,第一个if判断表示对应的节点均为null,返回true;若走到第二个条件,s与t当中有一个为null,返回false;最后再判断两个节点的值。
class Solution {
public boolean isSubtree(TreeNode s, TreeNode t) {
if(s == null) return false;
return isEqual(s, t) || isSubtree(s.left, t) || isSubtree(s.right, t);
}
private boolean isEqual(TreeNode s, TreeNode t) {
if(s == null && t == null) return true;
if(s != null && t == null || s== null && t != null) return false;
if(s.val == t.val) return isEqual(s.left, t.left) && isEqual(s.right, t.right);
return false;
}
}
在最坏情况下,对于s中的每个节点,我们都需要判断相应的子树与t是都相同,算法时间复杂度为$O(n\times m)$,其中n为s的节点数,m为t的节点数。空间复杂度即递归栈的深度为$O(n)$。
前序遍历s与t
第二种方式分别得到s与t的前序遍历字符串,判断t是否为s的字串即可。与一般的前序遍历不同的是,本题需要注意左右孩子为空的情况,需要使用特殊字符来标记空的左孩子与空的右孩子。举个例子说明,假设我们有如下两棵树:
1 1
/ \
1 1
可以得到s的前序遍历结果为11,t的前序遍历也为11,但是t却不是s的子树。如果我们用”lnull”与”rnull”分别标记空的左孩子与空的右孩子,则s的前序遍历变为11rnull,t的为1lnull1,此时后者的结果不是前者的字串。
class Solution {
public boolean isSubtree(TreeNode s, TreeNode t) {
String pres = preorder(s, true);
String pret = preorder(t, true);
return pres.indexOf(pret) >= 0;
}
private String preorder(TreeNode n, boolean isLeft) {
if(n == null) {
if(isLeft) return "lnull";
else return "rnull";
}
return "#" + n.val + preorder(n.left, true) + preorder(n.right, false);
}
}
后序遍历也可以做,但是中序遍历不行。另外空左节点与空右节点可以统一用”null”表示,不作区分也可。 分别遍历s与t时间复杂度为$O(n+m)$,indexOf复杂度为$O(n \times n)$,所以总的时间复杂度为$O(n+m+n \times m)$。当然判断子串也可以采用KMP这种复杂度为$O(m+n)$的方法。空间复杂度为两个递归栈深度的和$O(n+m)$。可以看到这种方式更加耗费内存,对于节点数多的树不太适合。