Stack and Queue - Notes
数据结构是用于在计算机中以结构化的方式存储数据以便有效处理数据的工具。高效的数据结构在设计高效的算法中起着至关重要的作用。例如在城市地图中,地标以及路网数据,使用二维平面来表示。本文回顾两个重要的数据结构,栈和队列,内容包含如何使用数组/链表实现栈和队列,如何用队列实现栈等部分。
Stack
栈是遵循LIFO/FILO的数据集合,LIFO即Last In First Out,FILO即First In Last Out,后进先出/先进后出原则。之所以称这种数据结构为堆栈,是因为它非常像现实世界的一副牌或一堆盘子。
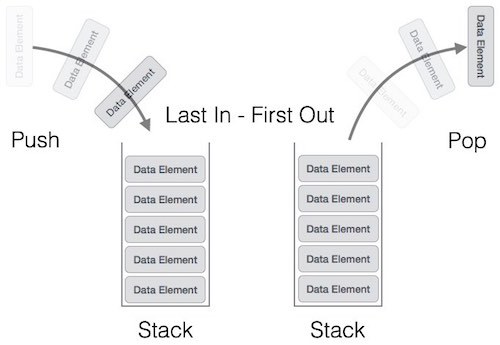
对栈的插入与删除只能在数据结构的一端进行,我们称之为top,顶部。插入元素操作叫做push,删除则为pop。Java与C++均提供栈的实现。Java的集合框架中Stack类继承Vector类。C++中STL也提供stack的实现,引入头文件#include <stack>即可。我们也可以子集实现一个栈。栈可以通过数组和链表实现,可以是固定大小的也可以是动态调整大小的。
在实现栈之前,首先定义栈的接口类,包含如下代码所示的一些基本操作。
public interface MyStack<Item> {
void push(Item item);
Item pop() throws Exception;
Item top();
boolean isEmpty();
int size();
}
数组实现栈
数组实现可以是固定大小的,即初始化的时候就给定数组的大小。也可以是动态调整的,涉及数组的重建与赋值。这里给出的是动态调整大小的数组实现栈。
public class ArrayStack<Item> implements MyStack<Item> {
private Item[] array = (Item[]) new Object[1]; //data array
private int n; //size
@Override
public void push(Item item) {
checkLength();
array[n++] = item;
}
@Override
public Item pop() throws EmptyStackException {
if(isEmpty()) {
throw new EmptyStackException();
}
Item item = array[--n];
checkLength();
array[n] = null;//防止内存泄漏
return item;
}
@Override
public Item top() {
if(isEmpty()) {
return null;
}
return array[n-1];
}
@Override
public boolean isEmpty() {
return n == 0;
}
@Override
public int size() {
return n;
}
/**
* 判断是否需要重新调整数组大小
*/
private void checkLength() {
if(n == array.length) {
resize(2 * array.length);
} else if(n > 0 && n < array.length / 4) {
resize(array.length / 2);
}
}
private void resize(int size) {
Item[] tmp = (Item[]) new Object[size];
for(int i = 0; i < n; ++i) {
tmp[i] = array[i];
}
array = tmp;
}
}
注意在实现pop方法时,被弹出的元素的引用实际上还存在于数组当中,这个元素实际上永远不会被访问了,但GC无法判断出是否要回收该元素,除非该引用被覆盖。为了防止“对象游离”,讲弹出元素的在数组中的引用置为null,GC即可对旧的引用进行回收。为了实现栈大小的动态调整,我们在每次push操作之前以及pop操作以后检查开辟的数组大小是否够用。如果栈大小已经等于数组大小,则重新创建一个2倍于旧数组大小的新数组;如果数组的利用率不高,比如n小于1/4的数组大小,则将数组大小缩小一半。
可以简单写个main函数测试一下自己实现的栈与java自带的栈的功能是否一致。
public class Main {
public static void main(String[] args) {
Stack<Integer> s1 = new Stack<>();
ArrayStack<Integer> s2 = new ArrayStack<>();
s1.push(1);
s2.push(1);
s1.push(2);
s2.push(2);
while (!s1.isEmpty()) {
System.out.println(s1.pop());
}
while (!s2.isEmpty()) {
System.out.println(s2.pop());
}
}
}
链表实现栈
如果采用链表结构实现栈,可以采用头插法(在之前的介绍单链表的文章中有介绍)。
public class LinkedListStack<Item> implements MyStack<Item> {
private class Node {
Item val;
Node next;
}
private Node top = null;
private int n = 0;
@Override
public void push(Item item) {
Node node = new Node();
node.val = item;
node.next = top;
top = node;
++n;
}
@Override
public Item pop() throws EmptyStackException {
if(isEmpty()) {
throw new EmptyStackException();
}
Item item = top.val;
top = top.next;
--n;
return null;
}
@Override
public Item top() {
if(isEmpty()) return null;
return top.val;
}
@Override
public boolean isEmpty() {
return n == 0;
}
@Override
public int size() {
return n;
}
}
Queue
与栈不同的是,队列是遵循FIFO(先进先出)原则的数据结构,即队列中先插入的元素先出队。这与现实生活中的排队现象是一致的。

队列支持入队,出队,返回队首元素操作。同样队列可以使用数组与链表实现,但是普通数组的实现比较低效,元素出队后无法重复利用内存(可以改进使用循环数组)。本文给出链表实现队列。事实上Java中的Queue也是LinkedList双向链表实现的。
public interface MyQueue<Item> {
void enqueue(Item item);
Item dequeue() throws Exception;
Item front();
int size();
boolean isEmpty();
}
链表实现队列
队列的链表实现需要维护first与last两个指针,分别指向队首与队尾。入队的时候需要考虑链表是否为空,若为空,说明插入的是第一个元素,队首队尾指向同一个元素。出队以后也需要判断链表是否为空,若为空,队尾指针设置为null。
public class LinkedListQueue<Item> implements MyQueue<Item> {
private class Node {
Item val;
Node next;
}
private Node first = null;
private Node last = null;
private int n = 0;
@Override
public void enqueue(Item item) {
Node node = new Node();
node.val = item;
node.next = null;
if(isEmpty()) {
first = node;
last = node;
} else {
last.next = node;
last = node;
}
++n;
}
@Override
public Item dequeue() throws Exception {
if(isEmpty()) {
throw new Exception("It's an empty queue");
}
Node node = first;
first = first.next;
--n;
if(isEmpty()) {
last = null;
}
return node.val;
}
@Override
public Item front() {
if(isEmpty()) return null;
return first.val;
}
@Override
public int size() {
return n;
}
@Override
public boolean isEmpty() {
return n == 0;
}
}
栈与队列的应用
栈与队列在树的各种遍历包括层次遍历以及前中后序遍历,图的深搜广搜以及字符串中都有很好的应用。
Valid Parentheses
括号匹配是一道经典的使用栈解决的题目,LeetCode简单难度20题。
给定一个只包含’(‘,’)’,’[‘,’]’,’{‘和’}’的字符串,实验一个函数判断括号是否匹配。匹配的条件是一个左括号必须有一个对应的右括号,并且顺序要对。 Example:
Input: “()”
Output: true
Input: “([)]”
Output: false
利用栈先进后出的性质,遇上左括号入栈,右括号出栈,判断是否匹配即可。
class Solution {
public boolean isValid(String s) {
if(s.isEmpty()) {
return true;
}
Stack<Character> stack = new Stack<>();
boolean valid = true;
for(int i=0; i<s.length(); ++i) {
char brancket = s.charAt(i);
if(brancket == '(' || brancket == '[' ||brancket == '{') {
stack.push(brancket);
}
else {
if(stack.isEmpty() || !isMatch(stack.pop(), brancket)) {
valid = false;
break;
}
}
}
if(valid) {
if(!stack.isEmpty()) {
valid = false;
}
}
return valid;
}
public boolean isMatch(char left, char right) {
if((left == '(' && right ==')') || (left == '[' && right ==']') || (left == '{' && right == '}')) {
return true;
}
return false;
}
}
利用队列实现栈/利用栈实现队列
LeetCode上两道设计题,队列与栈的互相实现对方。对于225题利用队列实现栈,考虑到队列是先进先出,栈是先进后出,往队列实现的栈中push一个元素时,元素被加到队列的队尾,所以需要反转整个队列满足栈的特性。
class MyStack {
LinkedList<Integer> queue;
/** Initialize your data structure here. */
public MyStack() {
queue = new LinkedList<>();
}
/** Push element x onto stack. */
public void push(int x) {
queue.push(x);
int size = queue.size();
while(size > 0) {
queue.add(queue.remove());
--size;
}
}
/** Removes the element on top of the stack and returns that element. */
public int pop() {
return queue.pop();
}
/** Get the top element. */
public int top() {
return queue.peek();
}
/** Returns whether the stack is empty. */
public boolean empty() {
return queue.isEmpty();
}
}
而针对232题利用栈实现队列,我们使用两个栈,push操作时,先把栈1的所有值pop掉,并push到栈2中,再将元素push到栈1。栈2的元素再依次push回栈1。这样操作的目的是是的push到队列的元素在尾部。
class MyQueue {
Stack<Integer> stack1;
Stack<Integer> stack2;
/** Initialize your data structure here. */
public MyQueue() {
stack1 = new Stack<>();
stack2 = new Stack<>();
}
/** Push element x to the back of queue. */
public void push(int x) {
while(!stack1.isEmpty()) {
stack2.push(stack1.pop());
}
stack1.push(x);
while(!stack2.isEmpty()) {
stack1.push(stack2.pop());
}
}
/** Removes the element from in front of queue and returns that element. */
public int pop() {
return stack1.pop();
}
/** Get the front element. */
public int peek() {
return stack1.peek();
}
/** Returns whether the queue is empty. */
public boolean empty() {
return stack1.isEmpty();
}
}
Min Stack
本题要求设计一个栈,支持push,pop,top以及在常量时间内获取栈的最小元素。
MinStack minStack = new MinStack();
minStack.push(-2);
minStack.push(0);
minStack.push(-3);
minStack.getMin(); --> Returns -3.
minStack.pop();
minStack.top(); --> Returns 0.
minStack.getMin(); --> Returns -2.
解决思路就是在最小值后面跟一个第二小的值,这样当最小值被pop时,下一个就是当前最小值,无需遍历栈重新计算最小值。
class MinStack {
private Stack<Integer> stack;
private int min;
/** initialize your data structure here. */
public MinStack() {
stack = new Stack<>();
min = Integer.MAX_VALUE;
}
public void push(int x) {
if(x <= min) {
stack.push(min);
min = x;
}
stack.push(x);
}
public void pop() {
if(stack.pop() == min) min = stack.pop();
}
public int top() {
return stack.peek();
}
public int getMin() {
return min;
}
}