Sorting Algorithms
排序算法几乎是每个程序员必须熟练掌握的算法,其可以用于数字,字符串,字符以及任何可比较的类型。排序算法有很多种,非常容易忘,故在此对常见的排序算法的思想以及实现做一个记录总结。本文涵盖冒泡排序,选择排序,插入排序,归并排序,快速排序,堆排序,基数排序七种排序算法。前六种是基于比较的排序算法,其算法复杂度由比较次数与交换次数决定。而基数排序只能应用于数字或字母。
| 算法 | 最好 | 平均 | 最差 | 空间 | 稳定 |
|---|---|---|---|---|---|
| 冒泡排序 | $O(n)$ | $O(n^2)$ | $O(n^2)$ | $O(1)$ | 稳定 |
| 选择排序 | $O(n)$ | $O(n^2)$ | $O(n^2)$ | $O(1)$ | 不稳定 |
| 插入排序 | $O(n)$ | $O(n^2)$ | $O(n^2)$ | $O(1)$ | 稳定 |
| 归并排序 | $O(n\log{n})$ | $O(n\log{n})$ | $O(n\log{n})$ | $O(n+\log{n})$ | 稳定 |
| 快速排序 | $O(n\log{n})$ | $O(n\log{n})$ | $O(n^2)$ | $O(\log{n})$ | 不稳定 |
| 堆排序 | $O(n\log{n})$ | $O(n\log{n})$ | $O(n\log{n})$ | $O(1)$ | 不稳定 |
| 基数排序 | $\small{O((n+b) * d)}$ | $\small{O((n+b) * d)}$ | $\small{O((n+b) * d)}$ | $\small{O(n+b * d)}$ | 稳定 |
Bubble Sort
冒泡排序的基本思想如其名字,不断地将最大/最小的数“冒”上去,重复比较相邻元素,如果大小顺序错误,则交换两数。图片credit:Animations of sort algorithms
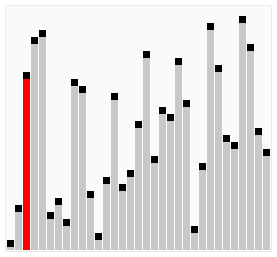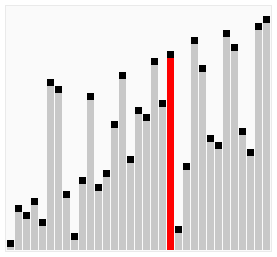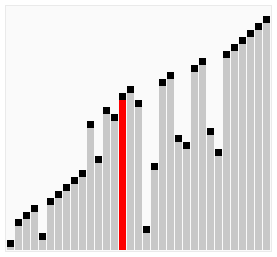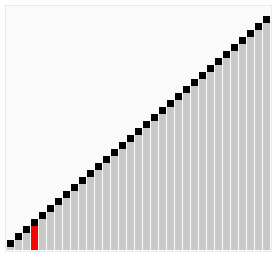
实现代码如下,当然也可以从数组末尾把最大/最小的数“冒”到数组头部,注意上下界即可。
void bubble_sort(int[] a) {
for(int i = 0; i < a.length-1; ++i) {
for(int j = 0; j < a.length-i-1; ++j) {
if(a[j] > a[j+1]) {
a[j] ^= a[j+1];
a[j+1] ^= a[j];
a[j] ^= a[j+1];
}
}
}
}
冒泡排序包含n趟n次交换,所以时间复杂度在平均和最坏情况为$O(n^2)$,即原数组为逆序;最好情况为$O(n)$,即原数组本身已经排好序,一次都不用交换。冒泡排序适用于数组大小比较小的情况。另外,冒泡排序是稳定的排序算法。
Selection Sort
选择排序算法基于在未排序数组中查找最小/最大元素然后将其放入排序数组中的正确位置的思想。以下图(Credit to Hackerearth)的数组[7,5,4,2]为例。
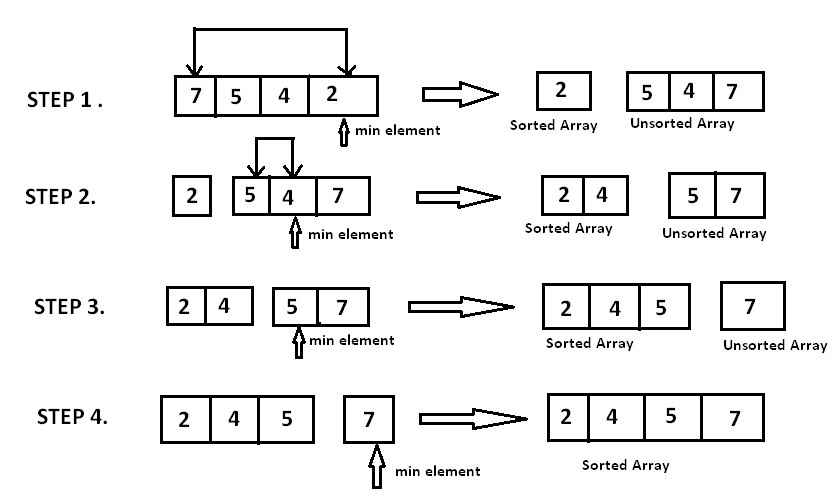
- 第一步,从位置
0开始找到最小元素与位置0元素交换,即2与7互换; - 第二步,从位置
1开始找到最小元素与位置1元素交换,即4与5互换; - 重复如此步骤,直到最后一个元素;
void selection_sort(int[] a) {
for(int i = 0; i < a.length-1; ++i) {
int min = Integer.MAX_VALUE;
int min_index = 0;
for(int j = i; j < a.length; j++) {
if(a[j] < min) {
min = a[j];
min_index = j;
}
}
a[i] ^= a[min_index];
a[min_index] ^= a[i];
a[i] ^= a[min_index];
}
}
选择排序在最坏情况和平均情况下,共需$(n-1)+(n-2)+…+1=\frac{n(n-1)}{2}$比较与$n$交换,所以时间复杂度为$O(n^2)$。与冒泡排序一样,最好情况是原数组本身有序,复杂度为$O(n)$。选择排序不是稳定的排序,相同元素的位置会改变。
Insertion Sort
插入排序每轮迭代为一个数找到正确的位置插入,正确的位置指的是在最终排好序的结果中的位置。假设当前迭代数的左边是排好序的,如果当前数大于左边最大数,则进行下一轮迭代;否则在左边找到合适的位置,插入该数。
void insertion_sort(int[] a) {
for(int i = 0; i < a.length; ++i) {
int temp = a[i];
int j = i;
while(j > 0 && a[j-1] > temp) {
a[j] = a[j-1];
--j;
}
a[j] = temp;
}
}
最差情况与平均情况下,每个元素做$n$次比较,时间复杂度为$O(n^2)$。
Merge Sort
归并排序是一种分治算法,其基本思想是将待排序数组分成长度更小的子数组,再将子数组排序后的结果合并得到最终的结果。
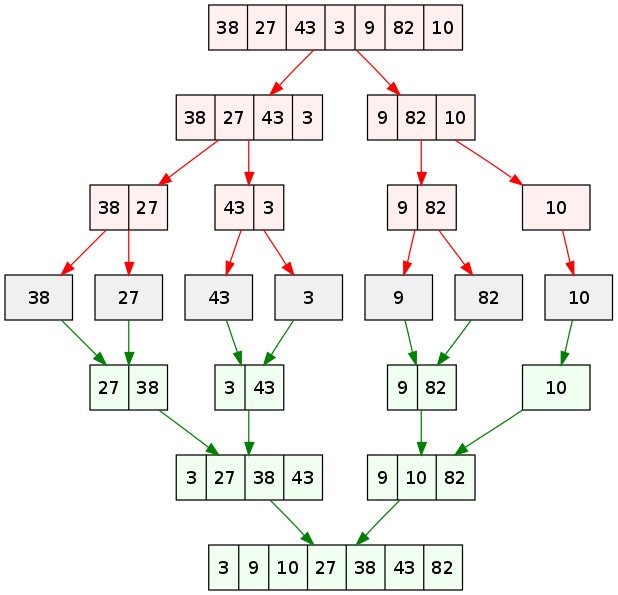
上图是对数组[38,27,43,3,9,82,10]应用递归的归并排序的具体过程,整个过程是自顶向下的。
- 首先不断的将数组从中间位置
mid分为两半,直到每个子数组只包含一个数,上图的第四层; - 之后再两个归并,例如
[38]和[27]归并为[27,38]; - 最后归并最开始的左右两部分;
归并的过程类似应用双指针,与LeetCode简单难度21题归并两个有序链表解法的思想一致。
void merge_sort(int[] a, int start, int end) {
if(start < end) {
int mid = start + (end - start) / 2;
merge_sort(a, start, mid);
merge_sort(a, mid + 1, end);
merge(a, start, mid, end);
}
}
void merge(int[] a, int start, int mid, int end) {
int p = start;
int q = mid + 1;
int[] temp = new int[end - start + 1];
int k = 0;
for(int i = start; i <= end; ++i) {
if(p > mid) temp[k++] = a[q++];
else if(q > end) temp[k++] = a[p++];
else if(a[p] < a[q]) temp[k++] = a[p++];
else temp[k++] = a[q++];
}
for(int j = 0; j < k; ++j) {
a[start++] = temp[j];
}
}
一颗包含n个节点的完全二叉树深度为$\log{n}$,又一趟归并需要扫描所有元素,故时间复杂度为$O(n\log{n})$。由于归并排序过程中需要新生成与原数组相同大小的数组以及递归深度为$\log{n}$的栈空间,故归并排序的空间复杂度为$O(n+\log{n})$。可以看出,归并排序效率较高,但是比较耗费内存空间。
Quick Sort
快速排序同样是一种分治的算法,该算法选择一个元素作为pivot,并围绕pivot将数组分为两部分,左边部分元素的值都小于pivot,右边元素都大于pivot。下图是快排算法流程示意图。
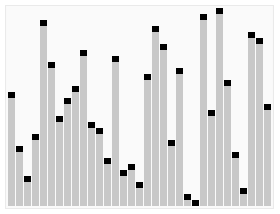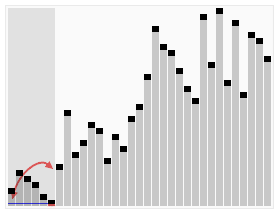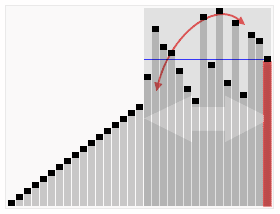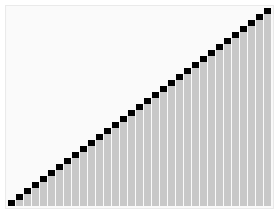
对于pivot的选择,我们可以直接选取第一个元素作为pivot,也可能随机选一个元素,与第一个元素交换作为pivot。代码中最关键的方法partition函数围绕pivot将数组分为两个子数组。j遍历数组,把小于pivot值的元素与i交换使得区间[start,i-1]的值都小于pivot。找到pivot正确的位置后,对左右部分递归地调用quick_sort。
int partition(int[] a, int start, int end) {
int i = start + 1;
int pivot = start; //选取第一个元素作为pivot
for(int j = start + 1; j <= end; ++j) {
if(a[j] < a[pivot]) { //交换,使得[start,i-1]都小于pivot值
a[i] ^= a[j];
a[j] ^= a[i];
a[i] ^= a[j];
++i;
}
}
//pivot放到正确的位置
a[pivot] ^= a[i-1];
a[i-1] ^= a[pivot];
a[pivot] ^= a[i-1];
return i-1;
}
void quick_sort(int[] a, int start, int end) {
if(start < end) {
int pivot = partition(a, start, end);
quick_sort(a, start, pivot - 1);
quick_sort(a, pivot + 1, end);
}
}
我们可以使用randompartition来代替原始的使用第一个元素作为pivot的partition来降低快排的时间复杂度。快速排序在最差情况下的时间复杂度为$O(n^2)$,平均情况与最好情况都是$O(n\log{n})$。另外,快排消除了归并排序中的辅助数组的空间开销$n$,所以其空间复杂度为递归栈空间的深度,即$O(\log{n})$。
Heap Sort
堆结构可以用来对数组进行排序,是一种基于selection的排序算法。首先我们看看堆结构长啥样。
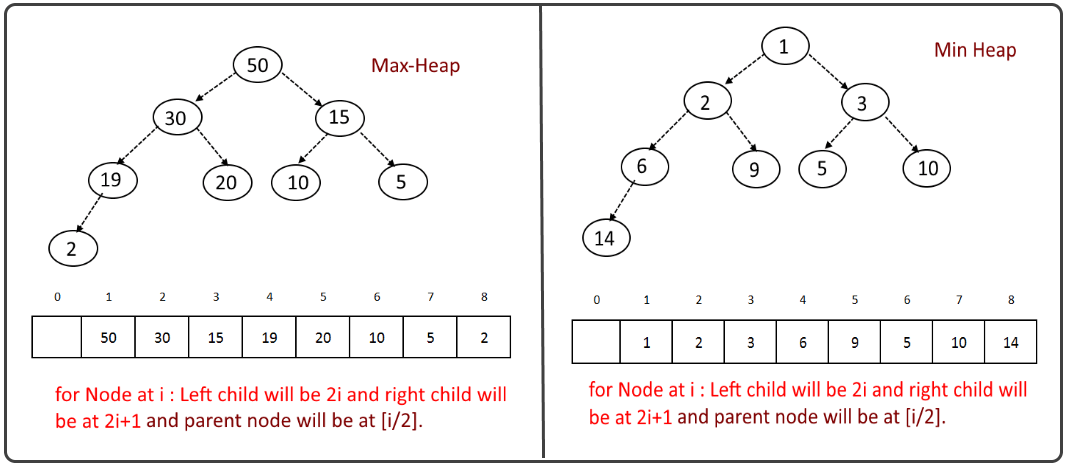
堆是一颗完全二叉树,大根堆的每个节点值大于其左右孩子节点的值,小根堆则小于其左右节点值。如上图所示,假设我们从堆顶开始,对节点按层进行编号(从1开始),一个堆可以映射为一个数组结构。并且数组有这样的性质,节点i的左右孩子节点分别为2i与2i+1(如果从0开始编号,则左右孩子为2i+1与2i+2)。
堆排序的基本思想是,首先构造一个大根堆(一般升序用大根堆,降序用小根堆)。大根堆的根是数组的最大值,接着将根与末尾交换,此时末尾就是最大值。然后剩余的节点重新调整成一个大根堆,如此反复得到一个有序数组。4分钟的视频给出了一个简单的堆排序的算法流程。
void heap_sort(int[] a) {
//build a max heap bottom-up
for(int i = a.length / 2 - 1; i >= 0; --i) {
heapify(a, i, a.length);
}
//swap heap root and the last element
for(int j = a.length - 1; j > 0; --j) {
a[0] ^= a[j];
a[j] ^= a[0];
a[0] ^= a[j];
heapify(a, 0, j);
}
}
void heapify(int[] a, int i, int size) {
int tmp = a[i];
for(int k = 2*i+1; k < size; k = k*2+1) {
if(k+1 < size && a[k] < a[k+1]) { //右节点大于左节点
++k;
}
if(a[k] > tmp) { // 左右节点较大值大于根节点值
a[i] = a[k];
i = k;
}
else {
break; //无需调整
}
}
a[i] = tmp;
}
堆排序主要有堆构建与交换堆顶与末尾并调整堆两部分开销。构建堆的开销为$O(n)$,而为每个节点与末尾做一次交换并调整堆的时间复杂度为$n\log{n}$。故堆排序的时间复杂度为$n\log{n}$,空间复杂度为$O(1)$。
Radix Sort
之前总结的如快速排序,归并排序和堆排序都是基于比较的排序算法。基数排序是桶排序的扩展,其基本思想是分割字符串或数字,根据相同位的键值分组进行一次稳定排序。基数排序一般有两种实现方式:
- MSD,从最高有效数字开始,通常适用于排序字符串,使用词典排序;
- LSD,从最低位数字开始,通常用于整数排序;
以LSD为例,对数组$10,21,17,34,44,11,654,123$应用低位优先的基数排序。首先根据个位数得到$1\underline{0},2\underline{1},1\underline{1},12\underline{3},3\underline{4},4\underline{4},65\underline{4},1\underline{7}$。接着按照十位数,我们有$\underline{1}0,\underline{1}1,\underline{1}7,\underline{2}1,1\underline{2}3,\underline{3}4,\underline{4}4,6\underline{5}4$。最后根据百位数,不足百位的补0,$\underline{0}10,\underline{0}11,\underline{0}17,\underline{0}21,\underline{0}34,\underline{0}44,\underline{1}23,\underline{6}54$。这样就得到最后排序的结果。
void count_sort(int[] a, int mul) {
int[] output = new int[a.length];
int[] buckets = new int[10]; //0-9
for(int i = 0; i < a.length; ++i) {
buckets[(a[i]/mul)%10]++;
}
for(int i = 1; i < 10; ++i) {
buckets[i] += buckets[i-1];
}
for(int i = a.length-1; i >= 0; --i) {
output[buckets[(a[i]/mul)%10]-1] = a[i];
--buckets[(a[i]/mul)%10];
}
for(int i = 0; i < a.length; ++i) {
a[i] = output[i];
}
}
void radix_sort(int[] a) {
int mul = 1;
int max = Arrays.stream(a).max().getAsInt();
while(max > 0) {
count_sort(a, mul);
mul *= 10;
max /= 10;
}
}
可以看到基数排序是多趟桶排序的实现。桶排序的时间复杂度为$O(n+b)$,其中n为待排序元素的个数,b为桶数目。趟数为$\log_{b}{max}$,例如最大数max为654,则趟数为$\log_{10}{654}$,即三趟。故基数排序的时间复杂度为$O((n+b) * \log_{b}{max})$。同理,空间复杂度为$O(n+b * \log_{b}{max})$。
当键很短时,基数排序效率比较高。但其依赖于数字和字母,灵活性比其他排序算法低。另外基数排序空间开销也比较大。